0. 서론
그래픽스를 공부하던 중 Anti-Aliasing에 대해 공부하게 되었는데 뭔가 머리에 잘 들어오지 않아 스스로 정리할 겸 SSAA와 MSAA, 이를 위한 샘플링 이론에 대해 정리한 글을 작성하고자 한다.
1. TL;DR
- Aliasing artifact를 줄이기 위해 SSAA와 MSAA 모두 원래 해상도보다 더 고해상도의 렌더 타겟을 이용한다.
- 따라서 SSAA, MSAA 모두 원래 해상도보다 큰 깊이 버퍼, 스텐실 버퍼 등을 필요로 한다.
- 그러나 SSAA는 고해상도 렌더 타겟의 크기만큼 픽셀 쉐이더를 호출하는 데 반해 MSAA는 원래 해상도 크기만큼 픽셀 쉐이더를 호출한다.
2. Aliasing
에일리어싱(위신호 현상, Aliasing)이란 연속 신호를 이산 신호로 샘플링하는 가운데 추출된 각 신호가 연속 신호를 정확히 표현하지 못해 발생하는 일종의 일그러짐(jaggies)을 의미한다. 대부분의 경우 ‘위신호 현상’이라는 용어 보다 ‘계단 현상‘이라는 용어에 더 익숙할 것이다.
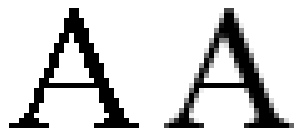
위 이미지의 왼쪽 A는 마치 블록들을 쌓아 만든 것처럼 각진 형태를 보인다. 이것이 바로 2차원 이미지에서 에일리어싱이 발생한 모습이다.
3. Anti-Aliasing
그렇다면 Anti-Aliasing은 무엇일까? Alising 앞에 ‘Anti’ 가 붙은 것에서 알 수 있듯 위에서 살펴본 에일리어싱 현상을 피하거나 완화하는 기법을 안티-에일리어싱(Anti-Aliasing)이라 한다.
잠시, 안티 에일리어싱에 대해 더 설명하려면 우선 Sampling과 Filtering의 개념에 대해 먼저 알아야 한다. 따라서 지금은 잠시 제쳐 두고 다음 개념들을 우선 살펴 보자.
4. Sampling, Reconstruction, Filtering and Resampling
Sampling
안티 에일리어싱은 적용하려는 신호의 구성에 따라 그 방법이 달라질 수 있지만 공통적인 아이디어를 가진다. 바로 “샘플링 주파수를 높이는 것”이다.
그렇다면 샘플링이란 무엇일까? 맨 처음 에일리어싱을 설명하며 언급했지만, 연속된 신호를 이산 신호로 변경하는 것을 말한다. 연속 신호를 이산 신호로 변경한다는 것은 연속 신호 중 일부 값들을 추출해 이들로 구성한 새로운 신호를 만든다는 것을 의미한다. 따라서 아래 도식과 같은 일이 일어난다.
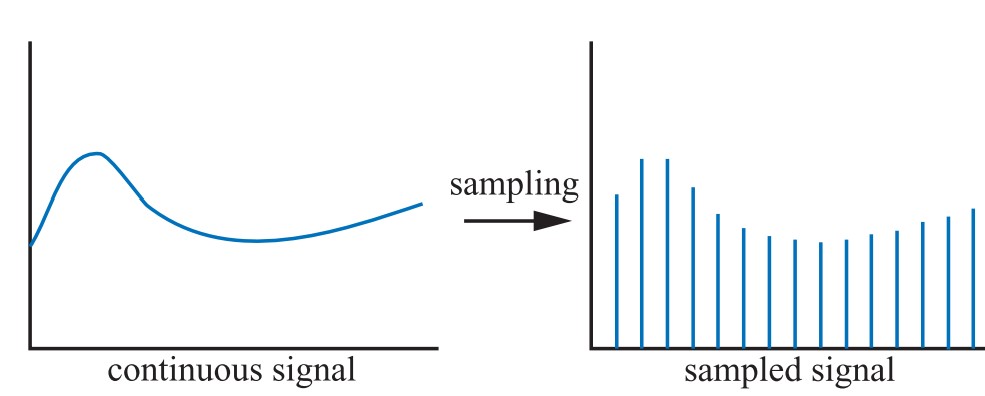 Real-time Rendering 4th edition, 131p
Real-time Rendering 4th edition, 131p
이렇게 샘플들을 추출할 때 중요한 것은 추출된 샘플들이 기존의 연속 신호를 잘 대변해야 한다는 것이다.
만약 샘플링이 제대로 수행되지 않았다면, 샘플들을 이용해 기존 데이터를 제대로 표현할 수 없게 되고, 이것이 바로 Aliasing이 일어나는 원인이 되는 것이다.
그렇다면 샘플링을 제대로 하기 위해서, 즉 Aliasing이 일어나지 않게 하기 위해선(이 포스트를 정독중이라면 이 말이 Anti-Aliasing을 의미함을 알 것이다) 어떻게 해야 할까?
신호 처리 이론에서, 원래 데이터의 최대 주파수(maximum frequency)의 2배 이상의 빈도로 샘플을 추출하게 되면 그 샘플들을 이용해 완벽히 이전의 연속 데이터를 재구성할 수 있음이 알려져 있다. 이를 샘플링 이론(Sampling theorem)이라 하며 제시된 빈도를 발견하신 선생님의 이름을 따서 나이퀴스트 빈도(Nyquist Rate)라 한다.
샘플링 이론에서 ‘최대 주파수’라는 용어가 나온 것으로부터 눈치챌 수 있겠지만, 이는 원래 신호가 대역 제한(band-limit)을 가질 수 밖에 없음을 의미한다. 즉, 특정 주파수를 초과하는 주파수가 없음을 의미한다.
그러나 3차원 공간이 Point Sampling을 통해 렌더링 될 땐 일반적으로 대역 제한을 갖지 않는다. 삼각형의 변이나 그림자의 경계, 하이라이트 조명의 경계 등은 이산적인 신호 변화를 만들어내므로 무한대의 주파수를 만들어내는 것과 동일하기 때문이다(쉽게 말해, 아무리 샘플 구간을 잘게 쪼개도 1->0으로 바뀌는 중간 지점을 캐치할 수 없다).
따라서 컴퓨터그래픽스에서 에일리어싱을 완벽히 제거한다는 것은 불가능하며, 단지 완화할 뿐이다.
Reconstruction
앞서 일반적인 경우 3차원 공간을 렌더링 할 때 대역 제한은 존재하지 않는다고 하였다. 그러나 특정한 경우 대역 제한을 확인할 수 있는데, 대표적인 예가 텍스쳐 샘플링이다. 한 Surface에 텍스쳐가 매핑될 때 텍스처의 주파수를 픽셀의 샘플링 비율과 비교해 얻어낼 수 있다. 만약 이 주파수가 나이퀴스트 빈도보다 높을 경우 이를 제한하기 위한 알고리즘들을 적용하게 된다.
이처럼 대역 제한된 샘플이 주어졌을 때 어떻게 이를 바탕으로 원래의 신호를 얻어낼 수 있을지를 알아보자. 이는 샘플을 통해 원래 신호를 재구성(Reconstruction)하는 것인데, 이를 위해 필터를 사용하며, 이러한 필터를 적용하는 것을 필터링(Filtering)이라 한다.
필터는 일종의 구간 함수인데, 특정한 샘플 영역에 씌워서 연속 신호를 만들어내는 모습으로부터 필터라는 이름이 붙여 졌다.
어떤 필터를 사용하는지에 따라 재구성된 신호의 형태가 크게 달라지는데, 가능한 재구성 신호가 연속이며, 미분 가능하도록 하는 필터가 좋은 필터이다. 이를 위해선 특정 폭 이상의 신호를 제거하는 형태의 필터가 필요한데, 이를 low-pass filter라 한다.
Resampling
연속 신호를 이산 신호로 바꾸는 것이 샘플링이고, 샘플들을 이용해 다시 연속 신호를 만들어내는 게 재구성임을 파악했으며, 재구성 과정에서 필터 함수들을 이용해야 하고 이를 적용하는 것을 필터링이라 하는 것 까지 정리해 보았다.
리샘플링(Resampling)은 샘플링된 신호의 주기를 증가시키거나 감소시키는 것을 의미한다. 예를 들어 1의 주기로 샘플링된 신호가 있을 때 이를 k의 주기로 샘플링된 신호로 변환시키고 싶을 때 수행하는 것이 바로 리샘플링이다.
이 때 만약 k가 원래 주기인 1보다 크다면 샘플의 수가 감소(minify)하게 되고 k가 1보다 작다면 샘플의 수가 증가(magnify)하게 된다.
샘플의 수를 증가시키는 것을 업샘플링(Upsampling)이라 하며, 이는 매우 간단하다. 필터링을 거친 결과에 샘플링 하는 지점을 늘리기만 하면 되기 때문이다.
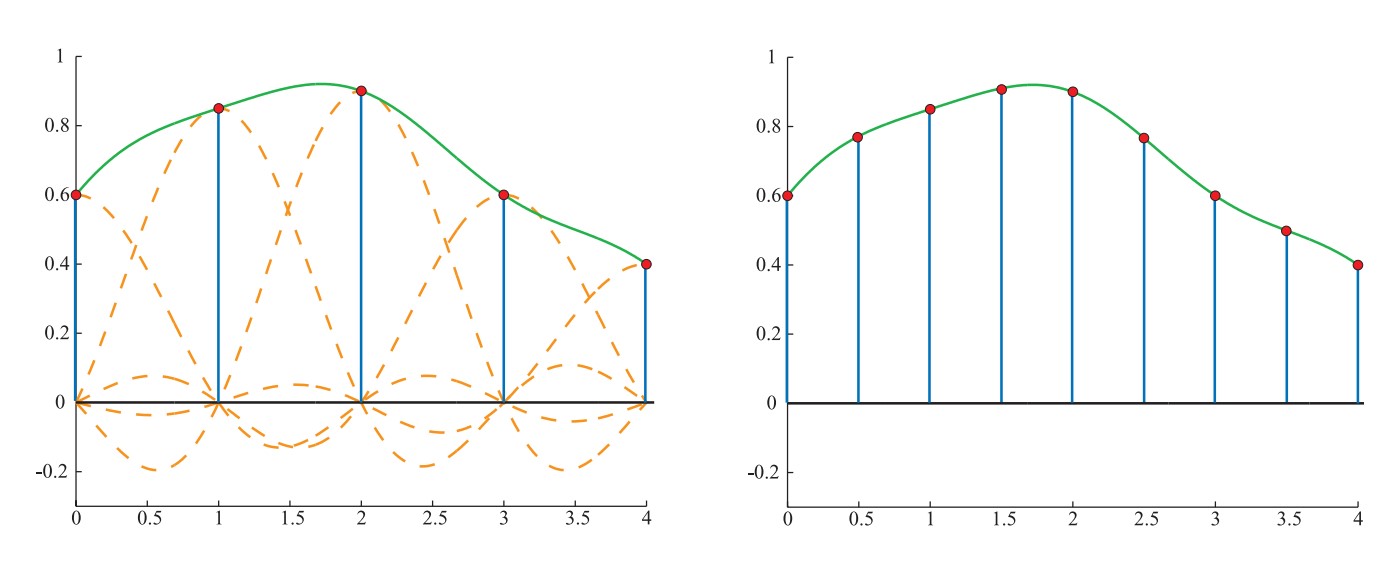 Real-time Rendering 4th edition, 137p
Real-time Rendering 4th edition, 137p
그러나 다운샘플링(Downsampling), 즉 샘플의 수를 감소시키는 것은 감소 과정에서 재구성을 거친 연속 신호의 특성을 잘 표현할 수 있도록 해야 하기 때문에 더욱 까다롭다.
일반적으로 샘플의 수를 감소시키는 경우에는 기존에 사용한 필터의 폭을 원하는 수준으로 늘려 필터링 하는 것으로 목표를 달성할 수 있다.
 Real-time Rendering 4th edition, 137p
Real-time Rendering 4th edition, 137p
5. SSAA
앞서 말했듯이 3차원 공간을 2차원 픽셀 공간으로 변환할 때의 최대 주파수는 존재하지 않기 때문에 완벽하게 에일리어싱을 없앨 수는 없다. 즉, 컴퓨터 그래픽스에서 완벽한 안티-에일리어싱 알고리즘은 존재하지 않는다. 따라서 안티-에일리어싱 만으로도 한 권의 책을 써낼 정도로 많은 알고리즘이 개발되어 왔지만 그들 각각은 자신의 장단점을 가지고 있기 때문에 자신의 어플리케이션에 어떠한 알고리즘을 적용할지는 상황에 따라 다르다.
그러나 대부분의 안티-에일리어싱 알고리즘은 Screen-based Algorithm이다. 즉, 2차원 픽셀의 색상값만을 이용해 알고리즘을 수행한다는 뜻이다. 또, 모든 AA 알고리즘의 공통적인 아이디어는 ‘한 픽셀의 색상을 결정하기 위해 주변의 여러 (서브)픽셀의 값들을 참조해 그들을 Blending해서 최종 색상을 결정한다’ 이다.
따라서, 여러 샘플링 패턴에 가중치를 부여하고 해당 패턴의 색상과 가중치의 곱을 합해 최종 색상을 결정한다. 이 때 모든 패턴의 가중치의 합은 1이다.
수식으로 나타내면 다음과 같을 것이다.
\[\textbf{p}(x, y) = \sum_{i=1}^{n} w_{i}\textbf{c}(i,x,y)\]여기서 $w_{i}$는 $i$번째 패턴의 가중치(weight)이며, $\textbf{c}(i, x, y)$는 $(x,y)$픽셀을 위한 $i$번째 샘플의 색상을 의미한다.
이처럼 한 픽셀을 결정하기 위해 둘 이상의 픽셀을 계산하는 AA 방식을 슈퍼샘플링(Supersampling)이라 한다.
SSAA는 Super Sampling Anti Aliasing을 의미하는데(FSAA, Full Scene Anti Aliasing이라고도 함), 그려낼 해상도보다 더 높은 해상도의 이미지에 3차원 공간을 그려낸 후 이를 원래 해상도로 압축하며 슈퍼샘플링을 수행하는 방식이다.
예를 들어, 1280x1024 크기의 이미지를 그려낸다고 할 때, GPU를 이용해 가로, 세로 2배 크기인 2560x2048 이미지를 먼저 그려낸 후 이를 압축하면 2x2픽셀 그리드가 최종 1픽셀을 결정하기 위해 이용되게 된다.
매우 간단한 컨셉이고 실제로도 구현하기 간단하지만, SSAA는 매 프레임마다 실제 이미지보다 n배 큰 이미지를 그려내야 하므로 픽셀 쉐이더의 호출 수도 n배 증가하게 되며, 프레임버퍼의 크기도 n배 증가하게 되므로 시/공간적 낭비가 크며, 그만큼 느리므로 실시간 렌더링에는 다소 적합하지 않다.
6. MSAA
SSAA가 느린 이유는 커진 해상도의 이미지를 모두 그려낸다는 점이 큰데, 이를 해결한 방법이 바로 MSAA이다. MSAA는 SSAA와 마찬가지로 고해상도 이미지를 렌더링한 후 이를 기반으로 샘플들을 추려내 각 픽셀의 최종 색상을 결정하지만, 이 과정에서 픽셀 쉐이더의 호출이 고해상도 이미지를 기준으로 하지 않고 원래 해상도를 기준으로 한다. 즉, 각 픽셀당 한 번의 픽셀 쉐이더를 호출한다.
따라서 고해상도 크기만큼의 프레임버퍼들이 필요한 것은 SSAA와 동일하지만 픽셀 쉐이더 호출 수가 훨씬 줄어들기 때문에 SSAA에 비해 빠른 동작을 보장받을 수 있다.
어떻게 고해상도 이미지에서 픽셀을 추출하는 방법을 한 번의 픽셀 쉐이더 호출로 이루어낼 수 있는지는…잘 모르겠다 ㅠㅠ 알게 되면 추가하겠다.
참고로, EQAA라는 알고리즘은 MSAA에서 색상 인덱스 버퍼를 추가하고 각 픽셀의 색상을 인덱스를 이용해 저장함으로써 필요 메모리 공간을 줄인 알고리즘이다. 그러나 MSAA에 비해 렌더링 품질이 좋지 않은 경우가 존재해 상위 호환적 알고리즘은 아니다.
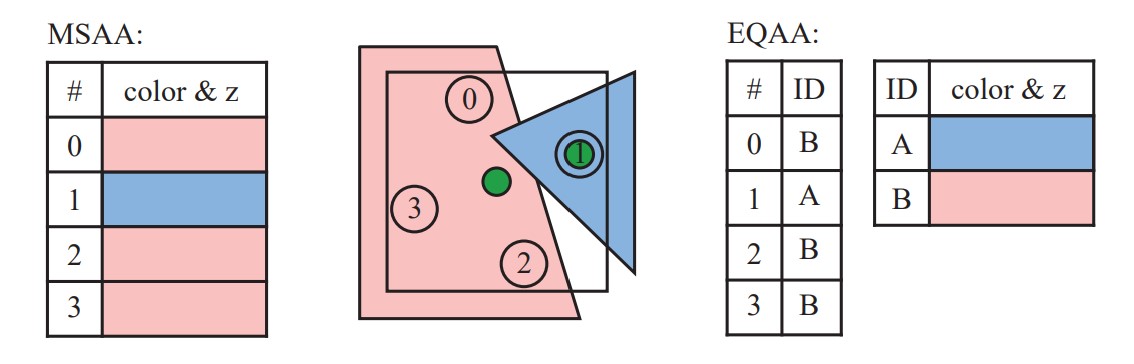 Real-time Rendering 4th edition, 141p
Real-time Rendering 4th edition, 141p