0. 서론
이번 주에는 싱숭생숭한 일이 많아서 프로젝트 개발에 많은 투자를 하지 못했다…
딱 하나 구현한 게 Bezier Curve다.
베지어 곡선을 구현한 이유는 이를 이용해 부드럽게 보간을 하거나, 카메라 워킹을 만들어낼 수 있기 때문이다(물론 이 외에도 여러 용도가 있다).
1. Bezier Curve
베지어 곡선은 셋 이상의 점을 이용해 곡선을 그리는(또는 곡선 형태로 보간하는) 방법이다.
곡선을 그리는 데 사용되는 점이 n개일 때 이를 n-1차 베지어 곡선이라고 하는데, 차수에 상관 없이 재귀를 이용해 구현되므로 굳이 차수를 나눌 필요가 없이 동일한 구현 방법을 가진다.
다만 굳이 고차원 곡선을 그리는 함수를 구현할 필요 없이 3차 베지어 곡선 정도면 충분히 원하는 모든 기능을 구현할 수 있겠다 싶어 3차 베지어 곡선 함수를 구현했다.
베지어 곡선은 드 카스텔조 알고리즘(de Casteljau algorithm) 을 통해 구현하는데, 드 카스텔조 알고리즘은 베지어 곡선을 구성하는 $n$개의 CP(Control Point)에 대해 동일한 매개변수 $t$에 대한 선형 보간을 수행하고, 그 결과로 나온 $n-1$개의 점을 새로운 CP의 집합으로 여겨 동일하게 $t$에 대한 선형 보간을 재귀적으로 수행하여 매개변수 $t$에 대한 곡선상의 점을 구하는 방법이다.
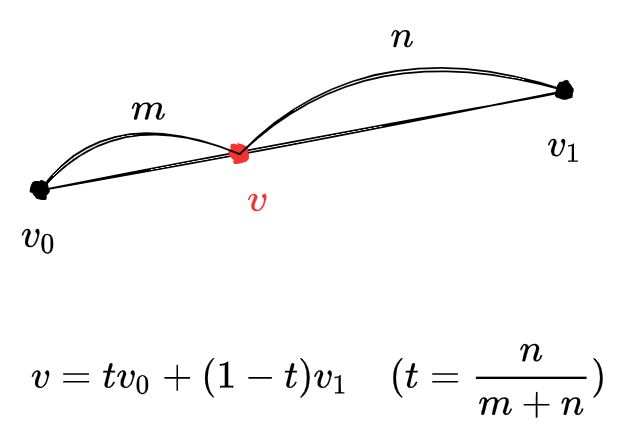
직선의 매개변수 표현은 위와 같이 가능한데, 이 때 매개변수 $t$를 $[0, 1]$ 범위에서 조정함으로써 선형 보간이 가능하다.
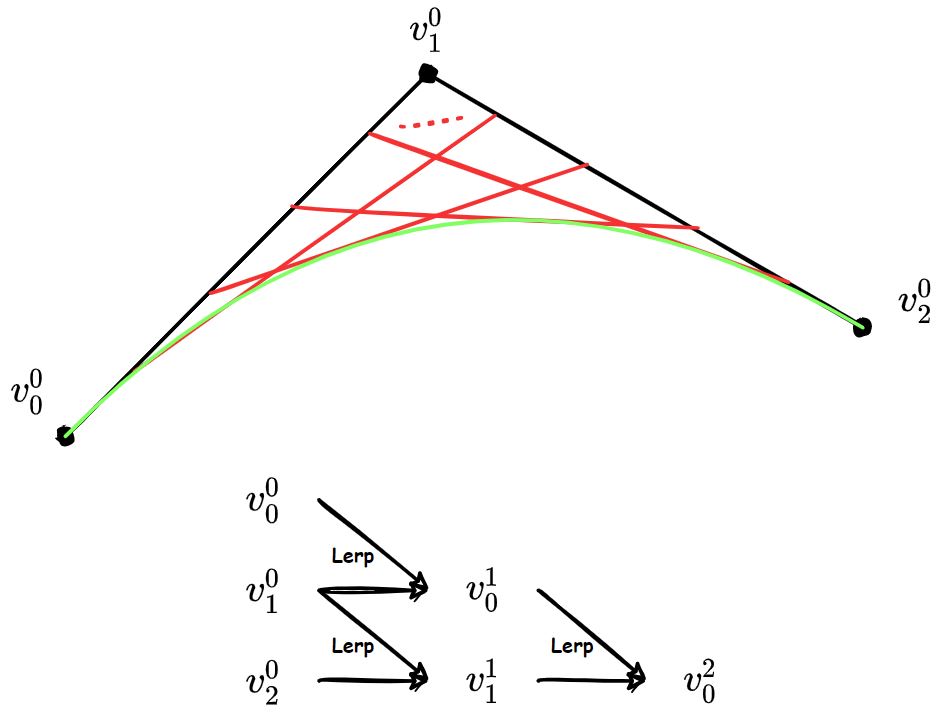
만약 2차 베지어 곡선이라면 $v$가 3개($v_0, v_1, v_2)$가 되는데, 각각의 $v_i$를 Control Point라 한다.
이 세개의 CP를 각각 매개변수 $t$에 대해 선형 보간하면 보간의 결과로 2개의 새로운 CP가 나오게 되고, 이 2개를 또 선형 보간하면 매개변수 $t$에 대한 베지어 곡선상의 점 $B(t)$가 나온다.
재귀적 수행을 쉽게 알아보기 위해 그 깊이를 위첨자로 작성한 후 도식으로 표현하면 다음과 같다.

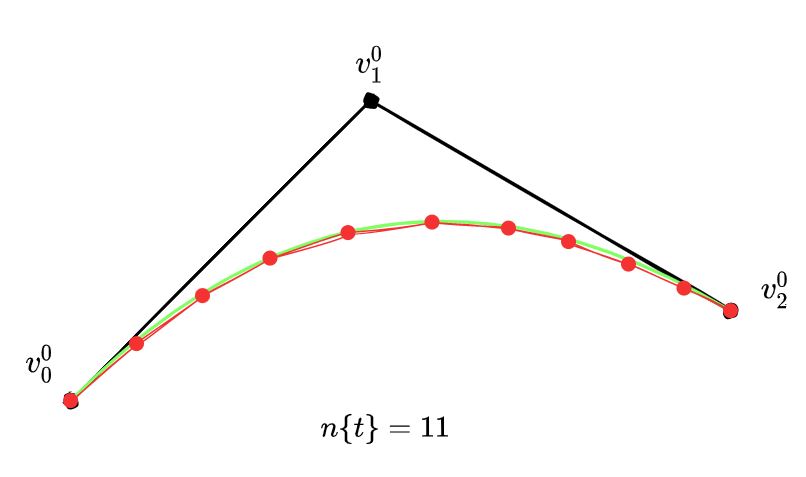
이 과정을 $[0, 1]$의 범위 안에 존재하는 실수 $t$에 대해 수행하면 다음과 같은 결과를 얻는다.
다만 이 과정을 구간 내의 모든 실수에 시도하는건 불가능하므로, 충분히 곡선을 표현할 수 있을 정도의 이산적인 t의 집합을 정해 해당 t에 대해서만 수행하게 된다. 이렇게 주어진 최초의 CP 집합 이용해 이산적인 t의 집합을 만들어내는 과정을 테셀레이션(Tessellation) 이라 한다.
2차 베지어 곡선에 대한 지금까지의 설명과 완전히 동일하게 3차 베지어 곡선도 그려낼 수 있다.

결론적으로, 프로젝트 상에서 3차 베지어 곡선은 다음과 같이 구현하였다.
template <typename T>
Vector3D<T> Bezier(Vector3D<T> v0, Vector3D<T> v1, Vector3D<T> v2, Vector3D<T> v3, float t)
{
Vector3D<T> v10 = Lerp(v0, v1, t);
Vector3D<T> V11 = Lerp(v1, v2, t);
Vector3D<T> v12 = Lerp(v2, v3, t);
Vector3D<T> v20 = Lerp(v10, v11, t);
Vector3D<T> v21 = Lerp(v11, v12, t);
return Lerp(v20, v21, t);
}위 코드를 이용해 큐브를 곡선 형태로 움직이는 데 성공했으며, 링크에서 확인할 수 있다. 여기서 움직이는 대상만 큐브에서 카메라로 바꾸면 아름다운 카메라 워킹이 구현된다.
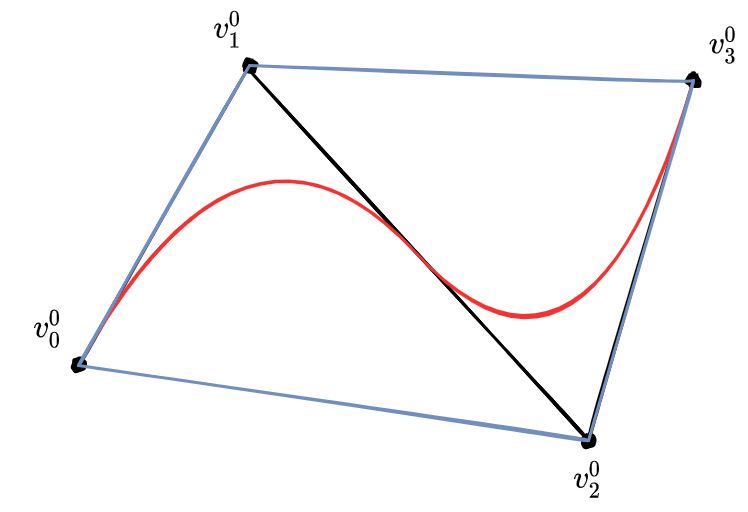
하나 더, 간단하지만 눈여겨 보면 베지어 곡선의 성질을 하나 알 수 있는데, 베지어 곡선은 반드시 CP들로 구성된 Convex Hull 내부에 위치한다는 것이다.
2. 결론
다음 주에는… Direct3D 11 개발도 같이 해서 더 시간이 없을 것 같다. 6월까지는 그래픽스 기법들을 최대한 구현해보고 싶은데.. 마음이 힘드니까 몸이 안따라준다. 그래도 힘내야지.