0. 문제

1. 풀이
학생들이 점심을 먹기 위해 일렬로 서 있을 때 줄 안의 특정 지점에서 콘서트를 열면 모든 학생들이 콘서트를 구경하러 오게 되는데, 이 때 모든 학생들이 콘서트에 참가하기 위해 최소한으로 움직일 수 있는 콘서트 지점을 구하는 문제이다.
따라서, 만약 줄 안에 학생이 단 한 명만 있다면 그 학생이 콘서트를 들을 수 있는 범위 안에서 콘서트를 열면 학생이 전혀 움직일 필요가 없으므로 이동거리가 최소($0$)가 되어 정답이 되는 것이다.
콘서트를 개최하는 위치 $P$ 와 $P$ 에서 콘서트를 열었을 때 학생들이 이동해야 하는 거리 총합을 함수 $f(P)$ 로 표현할 수 있는데, 이렇게 표현하게 되면 문제의 조건을 함수 그래프로 그려낼 수 있다.
예를 들어, 문제의 첫 번째 예시는 다음처럼 나타낼 수 있다.
1
0 1000 0

학생이 단 한 명이고, 해당 학생이 콘서트를 들을 수 있는 범위가 $0$이기 때문에 학생이 위치한 바로 그 지점에서 콘서트를 열면 이동 거리 합이 $0$이 되므로 정답이 된다.
동일한 방식으로 두 번째 예시는 다음처럼 나타낼 수 있다.
2
10 4 3
20 4 2
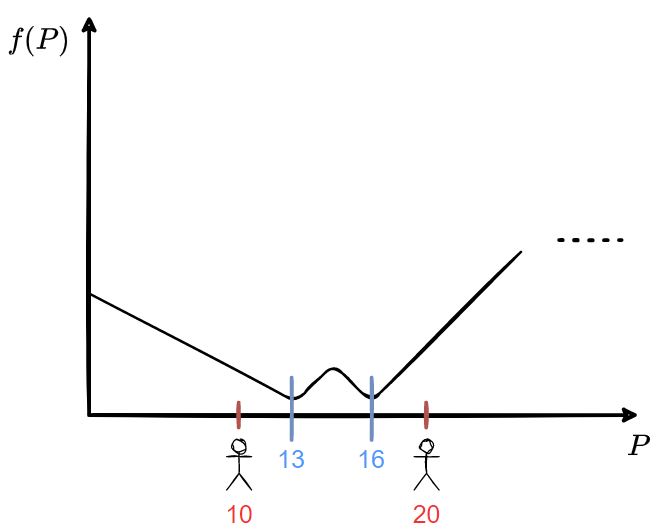
두 번째 예시에선 학생이 두 명이고, 각각 $10$ 과 $20$ 에 위치하는데, 공교롭게도 $f(13)$과 $f(16)$이 같이 최솟값을 가진다.
따라서 이 문제는 함수 $f(P)$를 구해 해당 함수의 최솟값을 출력하면 되는 문제이다.
이렇게 최솟값이 존재하는 함수(대표적으로 이차 함수)의 최솟값을 구해내고자 하는 경우 삼분 탐색(Ternary Search) 가 유용하게 이용된다.
이분 탐색이 범위를 절반씩 줄여 나가면서 원하는 지점을 탐색하는 알고리즘이라면, 삼분 탐색은 범위를 $\frac{1}{3}$씩 줄여 나가면서 원하는 지점을 탐색한다.
간단히 예를 들자면
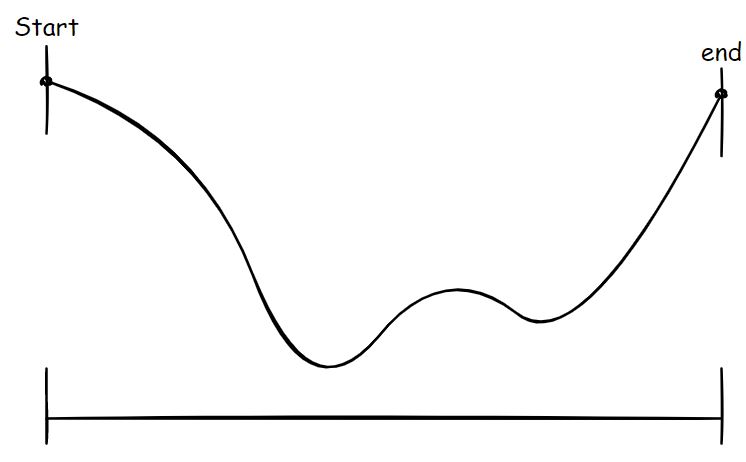
임의의 최솟값이 존재하는 함수 $g(x)$가 다음과 같을 때, 범위 $x$를 $\frac{1}{3}$씩 나누어 준다.

이후 $g(leftmid)$와 $g(rightmid)$를 비교해 $g(leftmid)$가 더 크다면 end를 right-mid로, 그렇지 않다면 start를 left-mid로 옮긴다.

이후, 위 알고리즘을 반복한다.

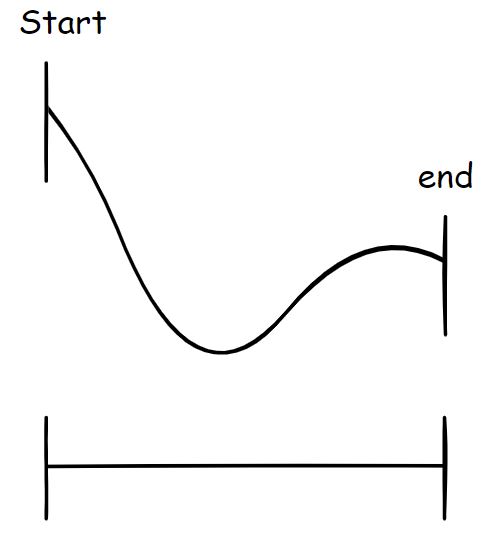
삼분 탐색을 알고 있던 사람이라면 위 설명을 듣고 의아할 수 있는데, 일반적인 삼분 탐색(함숫값을 찾는 것이 아닌 정렬된 데이터에서 값을 찾는 용도)의 경우 left-mid 와 right-mid 가 같은 값을 가질 경우 start, end 모두를 수정하지만, 이 문제는 $g(x)$가 정렬되어 있지 않기 때문에 다음과 같은 반례가 있을 수 있다.
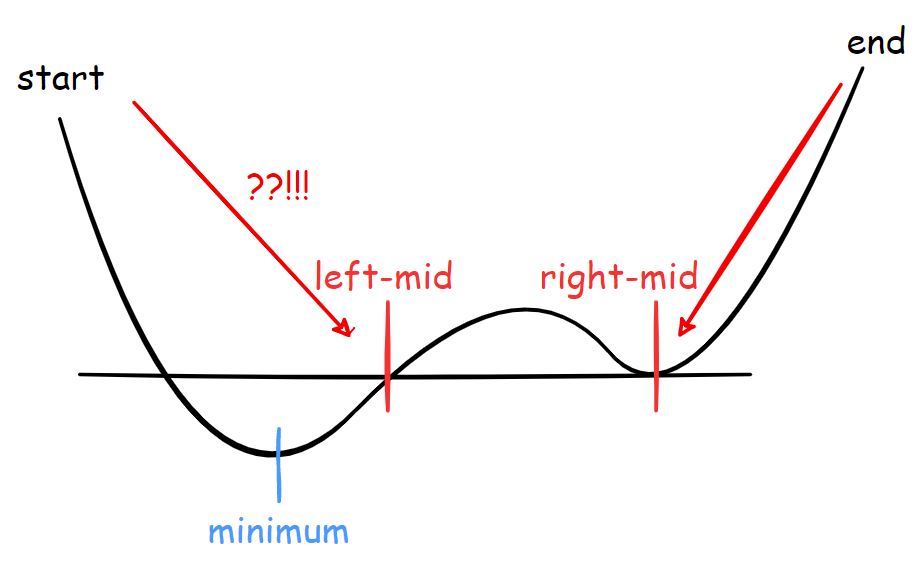
마찬가지로, 최솟값이 유일하지 않을 수 있다는 반례 때문에 일반적인 삼분 탐색처럼 start가 end보다 작거나 같은 동안 탐색을 계속 반복하는 방식은 무한 루프를 유발할 수 있다(두 학생이 $30$과 $31$에 서 있다고 상상해 보자). 그러므로 최솟값을 찾을 수 있을 정도의 충분한 횟수만큼만 삼분 탐색을 반복하도록 루프를 설정해야 한다.
2. 코드
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <cmath>
using namespace std;
constexpr int MAXN = 200'001;
constexpr int MAXD = 1e9;
int n;
int p[MAXN];
int w[MAXN];
int d[MAXN];
long long calc(int x)
{
long long sum = 0;
for (int i = 0; i < n; i++)
{
if (abs(x - p[i]) <= d[i])
{
continue;
}
long long hearingDist = min(abs((x - d[i]) - p[i]), abs((x + d[i]) - p[i]));
sum += hearingDist * (long long)w[i];
}
return sum;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
//freopen("input.txt", "r", stdin);
cin >> n;
int s = MAXD;
int e = 0;
for (int i = 0; i < n; i++)
{
cin >> p[i] >> w[i] >> d[i];
s = min(s, p[i]);
e = max(e, p[i]);
}
if (n == 1)
{
cout << 0;
return 0;
}
long long sum = 1e18;
for(int i=0;i<60;i++)
{
int delta = (e - s) / 3;
int l = s + delta;
int r = e - delta;
long long lr = calc(l);
long long rr = calc(r);
sum = min(lr, sum);
sum = min(rr, sum);
if (lr > rr)
{
s = l;
}
else
{
e = r;
}
}
cout << sum;
return 0;
}3. 결과
