0. 문제

1. 풀이
문제의 자료구조는 주어진 그림에서도 알 수 있듯이 방향그래프(Digraph) 로 표현 가능하며, 사이클이 존재하지 않는 방향 그래프(DAG, Directed Acycling Graph)이다.
또한 건물의 개수 N이 최대 1000개이므로, 정점의 개수가 최대 1000개인 DAG로 생각할 수 있다.
문제 예시의 2번째 상황을 DAG로 표현하면 다음과 같은데,

그림으로 그려 놓으면 해결하는 방법이 간단히 정리된다.
- 가장 기초 건물(선행 건물이 없는)부터 시작해서 테크트리대로 건물을 지어 나간다.
- 둘 이상의 건물이 선행되어야 지을 수 있는 건물(위 도식에선 7번 건물)은 필요한 건물들 중 최대 건설 시간을 가진 건물이 지어진 직후 지어진다.
따라서, 선행 정점이 없는 정점들부터 그래프 탐색을 하며, 각 정점의 비용을 갱신하되 갱신된 정점 비용이 갱신 전보다 클 때에만 갱신하면 된다.
위 조건대로 문제의 두번째 예시를 따라가면 다음과 같다.
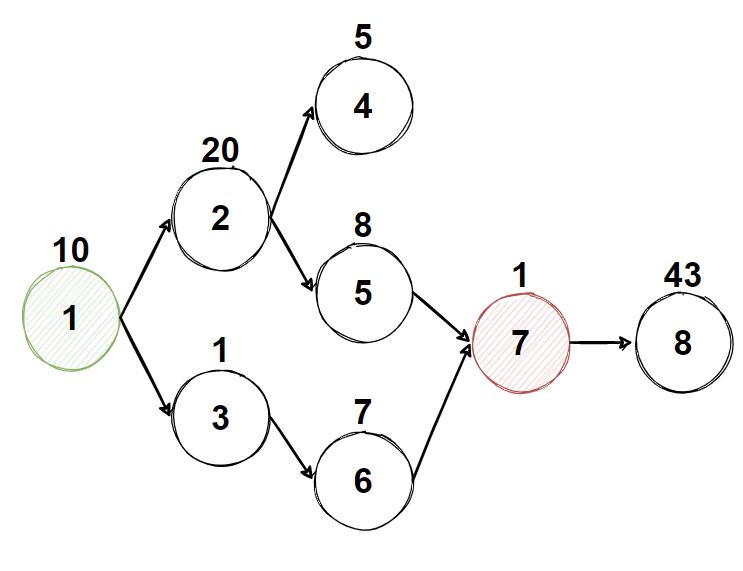
예시에서 기초 건물은 1번 뿐이므로 1번부터 시작하는 탐색 1번으로 정답을 알아낼 수 있다.
1번 정점은 갱신될 값이 없으므로 자신의 비용을 갱신 비용으로 똑같이 설정하고, 자신의 다음 정점(후행 노드)들을 너비 우선 탐색한다.
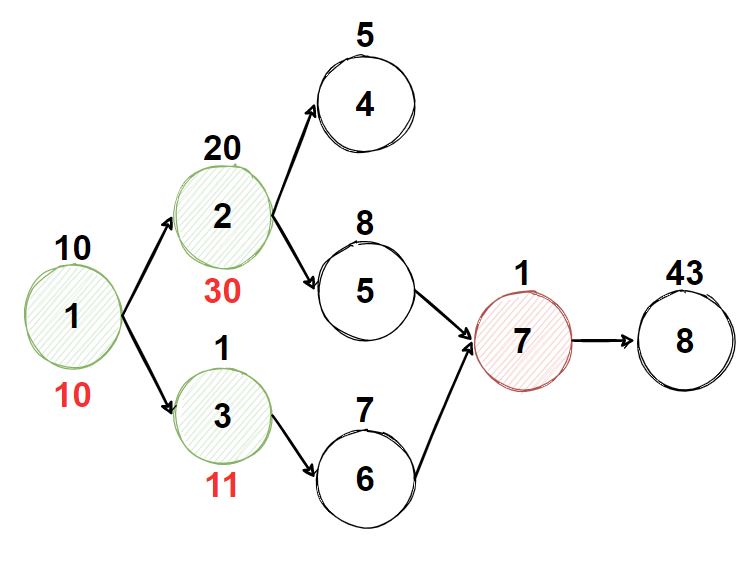
이때 2번과 3번 정점은 갱신 비용으로 자신의 정점 비용 + 선행 정점인 1번의 정점 비용을 설정한다.
그리고 같은 방법으로 너비우선탐색을 진행한다.

그 다음 탐색을 진행하려 했더니 7번 건물의 선행 건물이 둘 이상이다.
이 때에는 앞서 2. 방법에 따라 선행 건물들 중 가장 비용이 큰 건물을 기준으로 정점 비용을 갱신한다.
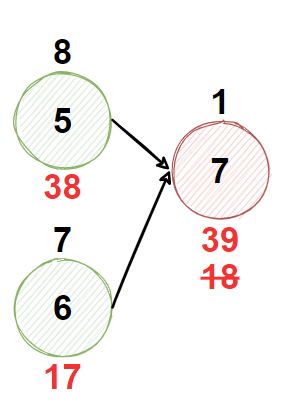
즉, 7번의 갱신 비용은 5번 정점의 갱신 비용 + 7번의 비용이 된다.
이러한 방법으로 끝까지 진행하면 탐색 결과는 다음과 같다.

이처럼 DAG의 각 정점들을 연결 관계에 따라 갱신하는 것을 다르게 표현하면 DAG를 연결 관계에 맞게 정렬한 후 선형으로 탐색하며 갱신하는 것으로 해석할 수 있고, 이러한 알고리즘을 위상 정렬(Topological Sort)이라 한다.
2. 코드
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>
#include <queue>
using namespace std;
constexpr int MAXN = 1001;
vector<int> graph[MAXN];
int pre[MAXN];
int cost[MAXN];
int dist[MAXN];
int main()
{
ios::sync_with_stdio(false);
cin.tie(nullptr);
//freopen("input.txt", "r", stdin);
int T;
cin >> T;
for (int tc = 1; tc <= T; tc++)
{
memset(graph, 0, sizeof(graph));
memset(pre, 0, sizeof(pre));
memset(cost, 0, sizeof(cost));
std::fill(dist, dist + MAXN, 0);
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++)
{
cin >> cost[i];
}
for (int i = 1; i <= k; i++)
{
int x, y;
cin >> x >> y;
graph[x].push_back(y);
pre[y]++;
}
queue<int> q;
for (int i = 1; i <= n; i++)
{
if (!pre[i])
{
q.push(i);
dist[i] = cost[i];
}
}
while (!q.empty())
{
auto cur = q.front();
q.pop();
for (int i = 0; i < graph[cur].size(); i++)
{
auto next = graph[cur][i];
if (dist[next] < cost[next] + dist[cur])
{
dist[next] = cost[next] + dist[cur];
q.push(next);
}
}
}
int w;
cin >> w;
cout << dist[w] << "\n";
}
return 0;
}3. 결과
