0. 서론
소프트웨어 래스터라이저(라 쓰고 렌더러라 읽음)를 구현하다가 삼각형을 벡터 방식으로 그리는 코드를 작성할 필요가 있었다.
삼각형 자체는 선분을 그리는 함수를 이용해 간단하게 그릴 수도 있지만, 삼각형 내부를 임의의 색으로 칠한다면 그렇게 단순하게 해결할 수가 없는데, 이때 삼각형을 구성하는 세 꼭지점(vertex)을 이용해 임의의 점이 삼각형의 내/외부 중 어디에 위치하는지 판단하는 방법을 알아보자.
1. 무게중심(Barycentric)
임의의 삼각형이 있을 때 삼각형의 무게 중심 $P$ 는 다음과 같다.
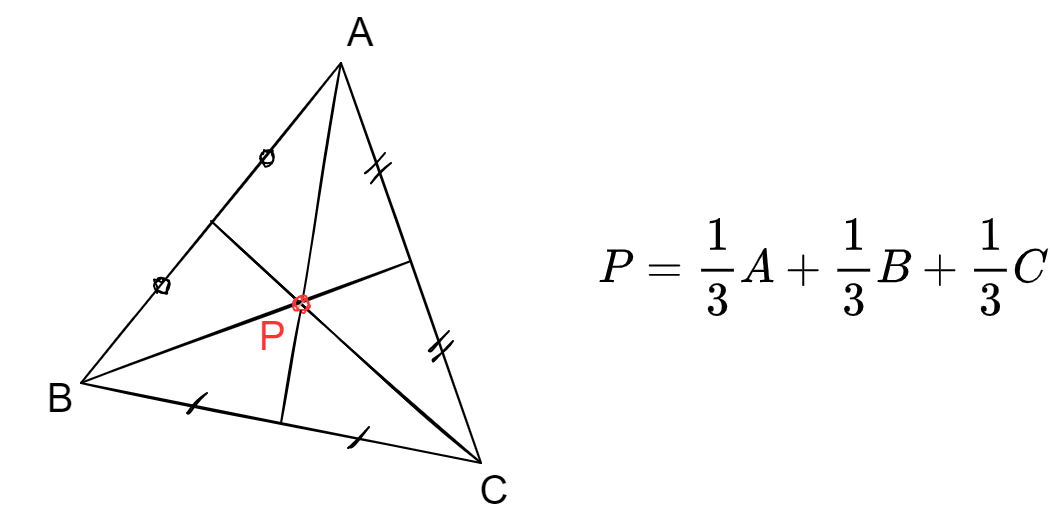
이때 점 $A$, $B$, $C$를 벡터로 해석하면 다음과 같이 표현된다.
\[\overrightarrow{P} = \frac{1}{3}\overrightarrow{A} + \frac{1}{3}\overrightarrow{B} + \frac{1}{3}\overrightarrow{C}\]간단하게 이를 증명하는 방법은 다음과 같다.
\[\overrightarrow{BM} = \frac{1}{2}\overrightarrow{BA} + \frac{1}{2}\overrightarrow{BC} 일\, 때,\\ \overrightarrow{BP} = \frac{2}{3}\overrightarrow{BM}이므로\\ \overrightarrow{BP} = \frac{2}{3}(\frac{1}{2}\overrightarrow{BA} + \frac{1}{2}\overrightarrow{BC})\\ =\frac{1}{3}\overrightarrow{BA} + \frac{1}{3}\overrightarrow{BC} \\ \\ 모든\;벡터의\; 시점을\; 원점 O로\; 옮기면(O는\; 생략) \\\\ \overrightarrow{P}-\overrightarrow{B} = \frac{1}{3}(\overrightarrow{A} - \overrightarrow{B}) + \frac{1}{3}(\overrightarrow{C} - \overrightarrow{B})\\ \overrightarrow{P} = \frac{1}{3}\overrightarrow{A}+\frac{1}{3}\overrightarrow{B}+\frac{1}{3}\overrightarrow{C}\]
2. 삼각형 내부의 점
앞서 살펴본 공식을 확장시키면, 삼각형 내의 임의의 점 $P$는 다음처럼 표현될 수 있다는 것을 안다.
\[P = (1-m-n)A + mB + nC\; (0 <= m+n<=1)\]이때 위 식을 벡터로 해석하고, 모든 벡터의 시점을 $P$로 놓으면 식이 다음처럼 표현된다.
\[\overrightarrow{0}=(1-m-n){\overrightarrow{PA}}+m\overrightarrow{PB}+n\overrightarrow{PC}\; (0<=m+n<=1)\]3. 대수적으로 접근하기
앞서 살펴본 삼각형 내부의 점 공식의 정리를 위해
\[p = \frac{m}{1-m-n},\; q = \frac{n}{1-m-n}\]로 치환하면 하면 임의의 점 P와 관계된 공식은
\[\overrightarrow{0} = \overrightarrow{PA} + p\overrightarrow{PB}+q\overrightarrow{PC}\]의 방정식 형태로 정리된다.
여기까지만 보았을 땐 $p$와 $q$ 두 개의 미지수를 하나의 방정식으로 해결하지 못할 것 같지만, 삼각형 자체가 2차원 도형이라는 것을 생각할 수 있다면(즉, 2차원 벡터들의 선형 결합으로 표현된다는 것을 생각할 수 있다면) 다음처럼 방정식을 두 개로 쪼갤 수 있다.
\[\begin{cases} \overrightarrow{PA}_x + p\overrightarrow{PB}_x + q\overrightarrow{PC}_x = 0\\ \overrightarrow{PA}_y + p\overrightarrow{PB}_y + q\overrightarrow{PC}_y = 0\\ \end{cases}\]4.외적을 이용한 연산
지금까지의 결과로도 충분히 방정식을 풀어 해를 알아낼 수 있지만, 조금 더 깊이 생각해볼 수 있다.
$\overrightarrow{PA}$, $\overrightarrow{PB}$, $\overrightarrow{PC}$의 $x$, $y$성분은 모두 스칼라이므로 연립방정식을 구성하는 각 식을 두 3차원 벡터의 내적으로 나타낼 수 있다.
\[\begin{cases} [1, p, q] \left[ \begin{matrix}\overrightarrow{PA}_x\\\overrightarrow{PB}_x\\\overrightarrow{PC}_x\end{matrix}\right] = 0\\ [1, p, q] \left[ \begin{matrix}\overrightarrow{PA}_y\\\overrightarrow{PB}_y\\\overrightarrow{PC}_y\end{matrix}\right] = 0\\ \end{cases}\]만약 내적의 기하학적 의미를 잘 알고 있다면 외적이 어떻게 사용될지 예상할 수 있을 것이다.
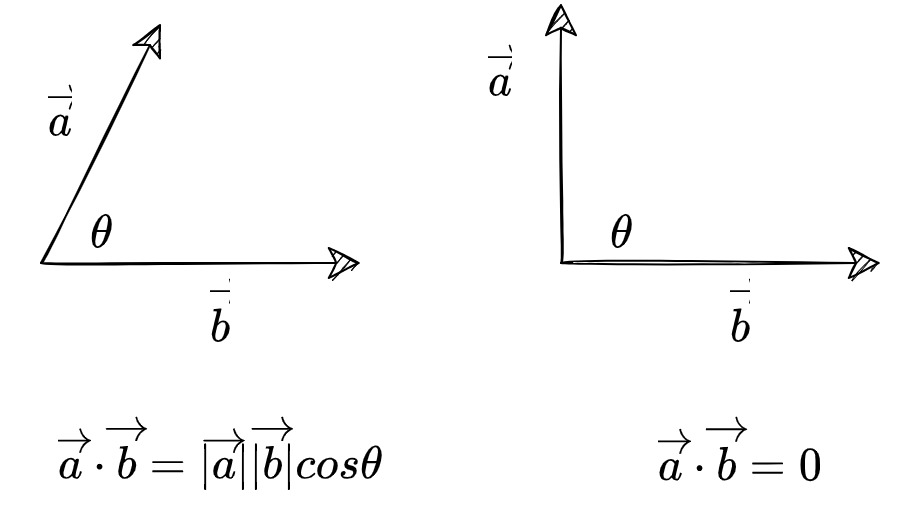
기하적으로 해석할 때, 두 벡터의 내적의 결과가 0이라면 두 벡터는 서로 수직이다.
즉, $\overrightarrow{x} = (\overrightarrow{PA}_x, \overrightarrow{PB}_x, \overrightarrow{PC}_x)$ 와 $\overrightarrow{y} = (\overrightarrow{PA}_y, \overrightarrow{PB}_y, \overrightarrow{PC}_y )$ 두 벡터는 모두 $\overrightarrow{p} = (1, p, q)$에 수직이다!
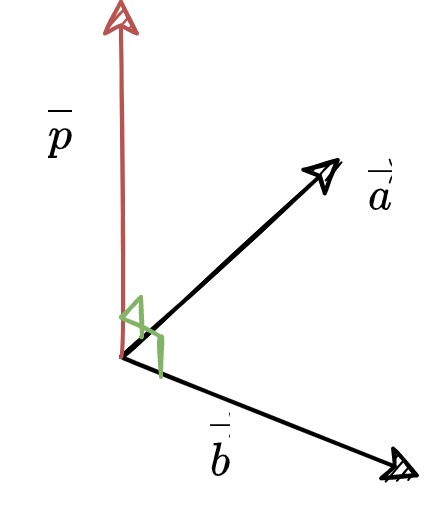
외적을 이용하면 두 벡터와 동시에 수직인(두 벡터를 기저로 하는 평면과 직교하는) 벡터를 얻을 수 있으므로 $\overrightarrow{x}$와 $\overrightarrow{y}$를 외적한 후 결과 벡터의 x성분으로 모든 성분을 나누면 그 결과가 위의 $\overrightarrow{p}$벡터임을 알 수 있다.
단, 이때 주의할 점은 외적의 결과로 나타난 벡터의 x성분이 0이면 안된다는 것이다. 따라서 벡터의 x성분의 절댓값이 0이라면 해당 좌표는 삼각형의 내부에 존재할 수 없다.
5. 결론을 코드로 나타내면
위의 결론을 의사 코드로 나타내면 다음과 같다.
function isInTriangle(Vec3 a, Vec3 b, Vec3 c, Vec3 p)
# initialize x, y vector
Vec3 x, y
x.x = a.x - p.x
x.y = b.x - p.x
x.z = c.x - p.x
y.x = a.y - p.y
y.y = b.y - p.y
y.z = c.y - p.y
Vec3 equation = cross(x, y);
if abs(equation) == 0 then:
return false
equation /= equation.x
if equation.x > 1 or equation.x < 0
or equation.y > 1 or equation.y < 0
or equation.z > 1 or equation.z < 0 then:
return false
return true6. 결론
소프트웨어 래스터라이저를 구현하다가 폴리곤의 구성 요소인 삼각형들을 어떻게 색칠할 수 있을까 고민하다 보니 이러한 결론을 낼 수 있었다.
위의 의사 코드에서 부울 대수를 반환하지 않고 equation 벡터를 이용하면 다음처럼 이쁜(?) gradiant triangle도 만들어낼 수 있다.
